Обоснование метода определения параметров нелинейной модели грунта по данным его полевых испытаний - Алехин Алексей Николаевич
Одной из центральных задач геотехники является разработка и применение эффективного и объективного метода расчета и проектирования плитного фундамента.
Объективного – в смысле адекватного учета физической природы грунтов основания и известных сложных особенностей взаимодействия с ним фундаментных конструкций сооружения.
Вспомнить хотя-бы недавнюю ситуацию, когда заказчик отказался выплатить строителям несколько миллионов рублей как раз из-за проблем с плитным фундаментом [1].
И такие проблемы, по-видимому, будут возникать все чаще по мере продвижения города в сторону мягких грунтов пригородов с гранитных массивов его центральной части.
Уже сейчас в Ботаническом районе города Екатеринбурга строятся несколько потенциально опасных с точки зрения надежности зданий.
Решение проблемы адекватного проектирования плитных фундаментов является еще и ключевым моментом решения проблемы совместного расчета системы Сооружение – Фундамент – Основание, как того требует статья 16 главы 3 Федерального закона №384-ФЗ «Технического регламента о безопасности зданий и сооружений.
Действительно, исключение из расчетов соединений элементов здания между собой не позволяет адекватно проанализировать и, следовательно, обеспечить прочность, надежность и требуемую жесткость этих соединений, определяемых, прежде всего особенностью взаимодействия элементов строительных конструкций между собой и с основанием, а также пространственной их работой.
Яркими следствиями подобных проектных упущений являются, например, такие аварии, как: обрушение конструкций спортивно-развлекательного комплекса «Трансвааль-парк» в Москве в 2004 году (Иллюстрация 1); обрушение конструкций покрытия бассейна «Дельфин» в городе Чусовом в 2005; обрушение кровли цеха в городе Екатеринбурге [2] в 1998 году.
Эти примеры в очередной раз указывает на опасность, увы, «модной» в последнее время среди инвесторов и проектировщиков тенденции игнорировать доскональное исследование, а если необходимо, то и дополнительную проверку инженерно-геотехнических условий площадки.
Участившиеся подобные факты стали, в том числе, одной из причин появления директивного в отличие от Строительных норм указания в вышеупомянутом Федеральном законе №384-ФЗ о необходимости учета реальных нелинейных, а не условных механических зависимостей грунта [2]. Ведь одна из главных механических характеристик грунта, используемая в геотехнических расчетах и называемая в механике грунтов «модулем деформации» фактически не существует.
Вообще-то механические характеристики грунтов, как деформационные, так и прочностные вслед за Л.Н. Репниковым [6] следовало-бы называть параметрами, поскольку, по сути, они являются параметрами принятых для данного конкретного вида нагружения (статического, динамического, циклического и т.д.) механических (прочностной, деформационной или их симбиоза) моделей грунта.

Иллюстрация.1. Обрушение конструкций спортивно-развлекательного комплекса «Трансвааль-парк» в городе Москва в 2004 году [3]
Это означает, что по своему виду и атрибутам эти величины, включая способы их определения и использования в расчетах, зависят от типа моделей.
Так в классической деформационной модели Фусса-Винклера (1798 год) жесткость грунта моделируется константой (называемой коэффициентом постели), которая связывает конечные перемещения поверхности грунта и давление на его границах (Иллюстрация 2). И это означает линейную зависимость между ними [4]. Тем самым, модель эта имеет статус лишь силовых условий на границе сплошной среды, отражающих ее общую сжимаемость в одном из направлений, но не определяющих автоматически особенности деформирования внутренних областей основания. Соответственно табличными значениями этих коэффициентов, особенно для ответственных сооружений, следует пользоваться с большой осторожностью (а лучше вообще не использовать из-за непредсказуемости результатов). В силу отмеченной методологической особенности модели Фусса-Винклера возникают известные затруднения с определением величин ее коэффициентов постели, а также проблемы использования этой модели, особенно при расчете влияния новой застройки на окружающие сооружения [5]. Для учета реальной жесткости, которая, как известно, является комбинацией сопротивлений изменению объема и формы, а также для учета особенностей основания необходимо определять искомый коэффициент постели на базе более общих моделей, способных отражать обе компоненты жесткости в любой точке активной зоны основания, т.е. зоны, испытывающей воздействие приложенной к нему нагрузки. В этом отношении классическая модель сплошной среды, которая как раз наиболее обоснованно применяется для этих целей, свободна от недостатков модели Фусса-Винклера [5]. При этом различные модификации модели Фусса-Винклера явились необходимым этапом на пути перехода к модели сплошной среды. Интересно, что интуитивно эти модификации были направлены главным образом как раз на добавку к компоненте сжатия сдвиговой компоненты [5]. Однако все модификации, довольно серьезно усложняя расчетные схемы, не решали главных проблем, прежде всего касающихся методов определения расчетных параметров моделей. На определенном этапе для определения коэффициентов постели (главным образом при проектировании плитных фундаментов), а также для самостоятельного применения в расчетах оснований сначала небольших фундаментов, а затем и плитных [6] стала использоваться модель сплошной линейно-деформируемой среды.

Иллюстрация 2. Графическая интерпретация модели Фусса-Винклера
Фактически эта модель является моделью Гука-Пуассона, соотношения которой обычно записываются в форме, так называемого, обобщенного закона Гука, связывающего компоненты тензора напряжений s и тензора относительных деформаций e:

Как следует из формул (1) жесткость грунта в рамках этой модели описывается двумя константами: модулем Юнга E (в механике грунтов его называют модулем деформации) и коэффициентом Пуассона n. Более современная и, как кажется, более содержательная форма этих соотношений записывается через инварианты тензоров, отражающих отдельно объемные деформации и деформации формоизменения (сдвига):
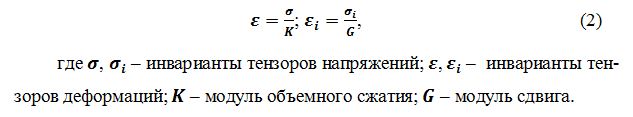
Здесь также жесткость моделируется двумя константами K и G, имеющими несколько иной смысл, чем константы E и n в формуле (1), но в комплексе и те и другие отражают один и тот же процесс деформирования, а потому допускают попарную взаимозаменяемость, например:
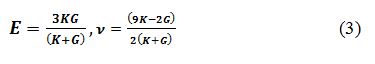
В любом случае постоянство этих величин, т.е. независимость их от напряженно-деформированного состояния (НДС) грунта означает линейный характер, содержащей их модели, а именно модели линейно-деформируемой среды.
Добавка к соотношениям (1) или (2) специфического закона прочности грунта в записи Кулона:

Графическая интерпретация этой системы приведена на Иллюстрации 4. Модель линейно-деформируемой среды сняла ряд существенных недостатков модели Фусса-Винклера [7]. Однако сравнение идеализированной диаграммы этой модели (Иллюстрация 3) с результатами фактических испытаний грунта в специальном исследовательском приборе для проверки теоретических грунтовых гипотез - стабилометре (Иллюстрация 4) показывает их существенное отличие (Иллюстрация 5).

Иллюстрация 3. Графическая интерпретация (диаграмма) системы линейных деформационно-прочностных моделей грунта,
описываемой формулами 2, 4, 5; на графике в скобках даны обозначения для версии Кулона (4)
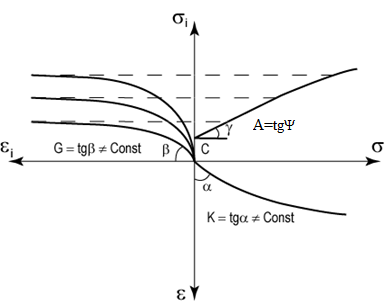
Главное отличие заключается в том, что реальное деформирование грунта значительно сложнее, чем это изображено на диаграмме Иллюстрации 3, и при этом характер деформирования существенно зависит от текущего НДС грунта. Впервые это экспериментально определил в 1939 году А.И. Боткин [8]. Он же весьма удачно применил для описания сложного девиторного нагружения (сдвига) грунта весьма эффективную гиперболическую формулу (6), которую затем в том или ином виде для описания деформаций грунта применяли многие другие авторы. Ниже приведены определяющие соотношения феноменологической нелинейной модели Боткина согласно ГОСТ 12248-96, с некоторыми ремарками, касающимися учета вида НДС [9].
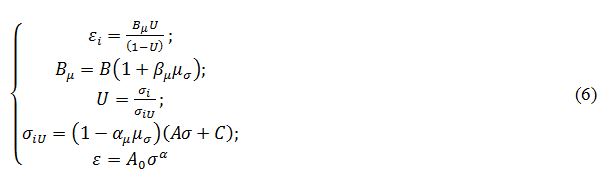
где σ – 1-ый инвариант тензора напряжений;
σi – 2-ой инвариант девиатора напряжений;
ε – 1-ый инвариант тензора деформаций;
εi – 2-ой инвариант девиатора деформаций;
σiU – предельное значение σi;
A=tg, B, C, A0, α, αμ, βμ – параметры нелинейной модели грунта; ремарки касаются главным образом учета вида НДС ms. На Иллюстрации 7 приведена упрощенная диаграмма модели Боткина в координатах инвариантов тензоров напряжений и деформаций как на диаграмме Иллюстрации 4.
В несоответствии линейной модели грунта его реальному деформированию заключаются все известные противоречия, возникающие при применении к расчету, прежде всего естественных оснований, теории линейно-деформируемой среды [9]. Характерно, что главное противоречие применения этой теории к грунтам заключается в том, что основной ее расчетный параметр – модуль Юнга (модуль деформации в механике грунтов) зависит от вида нагружения грунта. Таким образом, модуль деформации неинвариантен относительно НДС, а значит не может считаться параметром, т.е. константой грунта, как того требуют правила построения определяющих соотношений среды, т.е. ее модели. На такую условность грунтового модуля, по-видимому, впервые обратил внимание в 1967 году В.В. Лушников [10]. Хотя информация о влиянии на величину модуля, а также и коэффициента постели размеров и формы нагрузочных устройств (штампов) была известна еще в 1935 году Л.Н. Бернадскому [11], а еще раньше, в 1933 году немецкому геоинженеру Ф. Кёглеру [11].
Иллюстрация 4. Рабочая камера стабилометра
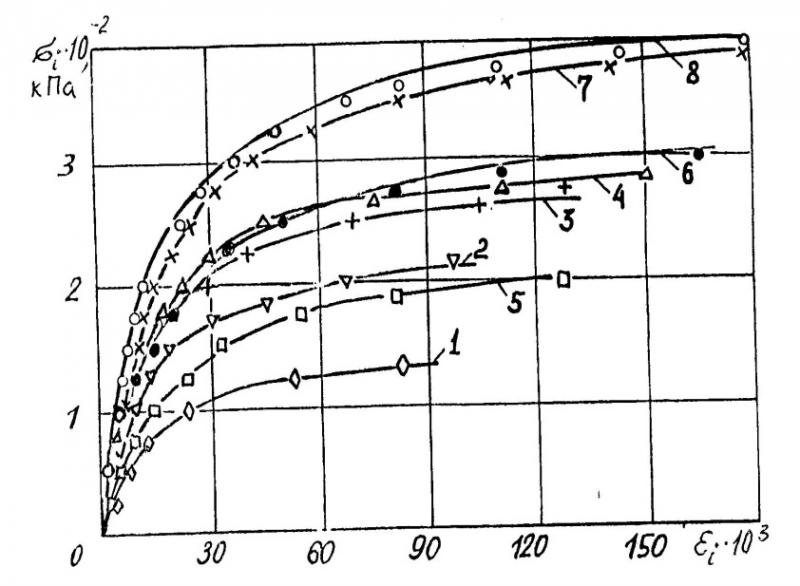
Иллюстрация 5. Девиаторная часть (σi – εi) протокола испытаний в стабилометре твердого элювиального суглинка ненарушенной структуры [7] (девиаторная ось εi для удобства анализа направлена вправо в отличие от диаграмм 4 и 7)
Иллюстрация 6. Упрощенная диаграмма нелинейной модели Боткина
Сравнение диаграмм Иллюстраций 3 и 6 с опытными данными на Иллюстрации 5 убедительно свидетельствует в пользу нелинейной модели Боткина, тем боле, что в оригинальном варианте модель Боткина имеет лишь на один параметр больше, чем в линейной системе Гука-Кулона (Иллюстрация 3). И этот параметр превращает линейный график в девиаторной области нагружения (σi – εi) в семейство кривых, определяющих всю гамму особенностей деформирования грунта в условиях монотонного статического нагружения грунтовых массивов [12]. Преимущества модели Боткина относительно линейной модели неоднократно широко обсуждались в специальной литературе и на различных конференциях, в том числе международных [2, 7,13]. При этом впервые на перспективность использования в расчетах нелинейных зависимостей Боткина и на хорошее совпадение результатов этих расчетов с экспериментальными данными еще в 1978 году указали В.С. Христофоров и Г.А. Задворнев [14]. Тем более, что как следует из диаграмм 4 и 7 нелинейная феноменологическая модель Боткина, по сути, является дальнейшим нелинейным обобщением также феноменологической модели Гука-Кулона. На базе этого вывода Христофоров и Задворнев предложили в 1979 году метод определения нелинейных параметров только несвязного (песчаного) грунта по данным прессиометрических испытаний, правда, используя для этого соотношения модели более низкого ранга, т.е. на базе линейной системы Гука-Кулона и приближенного одномерного решения прессиометрической задачи [15]. Очевидно, такая метода не могла давать надежные, устойчивые результаты. Поэтому, видимо, этот метод и не получил дальнейшего развития. Вместе с тем в методе были опробованы некоторые приемы решения некорректных задач [15], в частности использование дополнительной информации о соотношениях искомых параметров и особенностях нагрузочной схемы. И только через 20 лет исследований стало ясно, что задача определения реальных, в природном состоянии нелинейных параметров грунтов требует решения на первый взгляд довольно сложной обратной некорректной задачи механики сплошной среды [16]. Сложность постановки этой задачи легко понять из определения самого грунта: это хаотичный, сложный конгломерат твердых частиц различных размеров, формы и происхождения, в том числе органического, а также жидкостей и газов в пустотах грунта; при этом в расчетах грунт рассматривается в виде сплошной среды, бесконечно малая часть, которой идентична целому [2]. Вместе с тем революционное развитие вычислительной техники в конце XX века, позволило с приемлемой для проектирования и исследований скоростью решать сложные многомерные нелинейные задачи [17]. Это обстоятельство вкупе с удобным и, как отмечалось выше, весьма эффективным, в смысле описания реальной картины деформирования грунта, видом определяющих жесткостных соотношений А.И. Боткина, позволило с помощью дополнительных условий и с использованием всей совокупности опытных точек регуляризировать обратную неустойчивую задачу определения параметров. Как известно, именно эти два способа: использование дополнительной информации и увеличение количества опытных данных являются главными приемами повышения устойчивости некорректных задач [16]. Общая методика обработки данных полевых испытаний грунтов прессиометрами и штампами для определения параметров нелинейной феноменологической модели Боткина изложена в [7]. По мнению Л.Н. Репникова любая методика определения механических параметров грунта в полевых условиях должна быть обоснованной [5]. Следует добавить, что в случае обратной некорректной задачи под обоснованностью следует считать существование и единственность решения [16]. Покажем, что в случае определения параметров модели Боткина для решения проблемы применим широко распространенный в практике способ подбора.
Операторное уравнение прямой задачи определения перемещений грунта под действием приложенной нагрузки имеет вид:
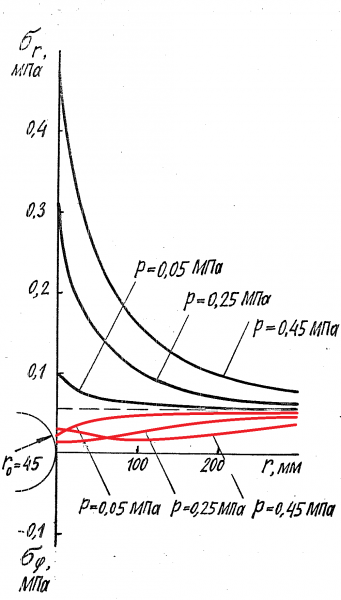
В силу сложности оператора A и неточности значений измеренных величин u прямая задача (7), вообще говоря, не имеет обратного решения, т.е. обратная задача z= A-1(u) является некорректно поставленной, неустойчивой к малым изменениям исходных данных. С другой стороны согласно утверждению Ж.Адамара [18] корректными могут считаться «естественные» задачи, описывающие существующие физические процессы. Поскольку процесс деформирования грунта при его нагружении не вызывает сомнения, задача определения механических параметров грунта, определяющих этот процесс может считаться, по крайней мере, потенциально корректной, т.е. хотя-бы поддающейся процессу регуляризации. Эта операция означает добавление условий задачи, позволяющих ее решить, например, путем уменьшения числа неизвестных в основном уравнении обратной задачи. Таких регулязирующих условий или операторов может быть несколько. В случае определения нелинейных параметров грунта ключевым условием является условие, вытекающее из подобия реальных и численно смоделированных графиков деформации грунта, о чем свидетельствуют как данные вышеупомянутой работы [14], так и материалы работы [12]. В работе [12] наряду с другими результатами имеется график, очень точно отражающий природу грунта. На Иллюстрации 7 приведено численно смоделированное расчетное распределение радиальных sr и тангенциальных sj напряжений в песчаном грунте вокруг скважины. На графиках хорошо видно, что при любом давлении p на стенки скважины тангенциальные напряжения sj в песке остаются сжимающими. Экспериментальное подтверждение чему, кстати, приведено в работе [14]. Заметим, что в упругопластических решениях приходится принудительно задавать условие равенства нулю тангенциальных напряженийsj для песка. Упомянутое условие подобия графиков было с одной стороны использовано для разработки метода прогноза осадки фундаментов [19], а с другой – метода определения наиболее важного деформационного параметра гиперболической функции для модуля сдвига в модели Боткина – параметра B [20]. Вообще в классическом построении модели Боткина присутствует, как указывалось выше, пять параметров – кроме параметра B еще параметры: A, C, A0, α, к которым могут быть добавлены параметры, учитывающие вид НДС. Согласно [20]:
Здесь: BL – лабораторное значение параметра B, а ΔUi и ΔUic (A, C, A0, α, B) – соответственно фактические и численно смоделированные значения перемещений грунта при прессиометрическом или при штамповых испытаниях; в случае раздельного использования данные и тех и других имеется возможность определения полевого значения коэффициента βμ (6) при параметре вида НДС (параметр Лодэ-Надаи μσ).
Очевидно, что согласно формуле (8) значение параметра В существует и единственно для конкретного полевого испытания. В работе [20] приводятся результаты независимого определения параметра B по двум графикам штампового испытания одного и того же грунта на разных глубинах. Отличие, как неудивительно, не превысило 3%, что свидетельствует в пользу высокой степени адекватности модели Боткина, учитывающей, в том числе, увеличение жесткости грунта с глубиной [12], т.е. об ее эффективности.
Приняв в дальнейшем алгоритме действительное число BÎ R, в качестве константы, мы тем самым переводим решение проблемы в область ограниченного множества натуральных чисел (AÎ N и CÎ N), поскольку нормативными геотехническими документами задано ограничение на величину угла внутреннего трения j: 5…45° с шагом 1° [21]. В принципе этот диапазон может быть даже расширен, но при современных технологических возможностях компьютеров это не имеет существенного значения. Значение же A является аналогом тангенса угла внутреннего трения j и связано с tg j константой, зависящей от вида НДС, то же касается соотношения удельного сцепления c и параметра Мизеса С [22]. Соотношение между параметрами Мизеса C и A такое же, как между c и tg j [22], а это последнее достаточно надежно определяется в испытаниях грунта на срез. Параметр кривизны графика объемных деформаций α в компрессионной области нагружения (σ – ε) определяется в компрессионном приборе и практически не отличается от полевого значения В этом случае для поиска решений некорректно поставленных задач эффективен метод подбора [16], который заключается в том, что для некоторого набора параметров (в данном случае A, B, C, α и полученного в компрессионном приборе приближенного значения параметра A0) решается прямая задача (7) и в качестве решения берется набор параметров z с минимальной невязкой ru (Az, u). Очевидно, что в силу существования решения прямой задачи такой набор параметров существует и единственен для конкретного полевого испытания, а в случае раздельного использования данных прессиометрических и штамповых испытаний, как и в случае с параметром B имеется также возможность определения полевого значения коэффициента aμ (6) при параметре вида НДС Лодэ-Надаи. Наконец на последнем этапе метода корректировка параметра A0 осуществляется стандартным методом минимизации, например, по методу наименьших квадратов невязки ru (Azk, u) по одному параметру zk = A0. При этом u – та же, что и в (7) совокупность измеренных в опытах величин. Поскольку в случае одного неизвестного параметра уравнение регрессии будет линейным, то существование и единственность искомого параметра A0, как и в случае остальных параметров также очевидны. Таким образом, в силу вышеизложенного предлагаемый метод определения параметров по данным полевых испытаний обеспечивает существование и единственность набора их значений, соответствующих фактическим данных этих испытаний, т.е. характеризующих реальные механические свойства исследованного грунта.
Иллюстрация 7. Графики радиальных sr (черный цвет) и тангенциальных sj (красный цвет) напряжений в песчаном грунте вокруг скважины при различном давлении p на ее стенку [12]
Заключение
- Приведенное в статье обоснование существования и единственности решения проблемы определения параметров одной из эффективных нелинейных моделей грунта по данным его полевых испытаний открывает возможность скорейшего внедрения нелинейных моделей в практику проектирования согласно положениям Федерального закона №384-ФЗ.
- Эти модели позволяют учесть в геотехнических расчетах две главные особенности грунтов: сложность их деформирования и природное происхождение.
- Для обеспечения экономической эффективности перехода в геотехническом проектировании от линейных моделей к их нелинейным аналогам на базе полевых испытаний грунтов следует также повысить технологичность и оптимизировать параметры полевых приборов, прежде всего размеры их нагрузочных частей.
Список использованной литературы
- Отчет №ТК-120 по результатам обследования технического состояния несущих и ограждающих конструкций здания многопрофильной клиники, расположенной на пересечении улиц Большакова – Чайковского в городе Екатеринбурге. / ООО «ТЕХКОН. – Екатеринбург, 2012. – 182 с.
- Алехин А.Н. Геотехнические аспекты Федерального закона №384-ФЗ «Технический регламент о безопасности зданий и сооружений» // Академический вестник УралНИИпроект РААСН – Екатеринбург: УралНИИпроект,2014. – №4. – С. 82 – 86.
- http://www.gazeta.ru/2004/02/14/box_3822.sht.
- Алехин А.Н. Краткая характеристика моделей грунта // Академический вестник УралНИИпроект РААСН – Екатеринбург: УралНИИпроект,2011. – №1. – С. 75 – 80.
- Репников Л.Н. Расчет конструкций на комбинированном основании. – М.: Стройиздат, 1973. – 128 с.
- Горбунов-Посадов М.И. Расчет конструкций на упругом основании. – М.: Госстройиздат, 1955. – 515 с.
- Алехин А.Н., Алехин А.А. Определение параметров нелинейной модели грунта по данным полевых испытаний / Геотехнические проблемы мегаполисов: Труды Международной конференции по геотехнике. – М., 2010 – С. 1201–1208.
- Боткин А.И. Исследование напряжённого состояния в сыпучих и связных грунтах // Изв. НИИ гидротехники. – М.-Л.: 1939. – т. XXIV. – С. 153 –172.
- Алехин А.Н. Критика применения теории линейно-деформируемой среды при расчете деформации грунтов// Проблемы градостроительства на Урале в 21 веке: Пятые Уральские академические чтения. – Екатеринбург: Российская академия архитектуры и строительных наук (Уральское региональное отделение), 2000. – С. 142 – 148.
- Лушников В.В. Сопоставление результатов полевых и лабораторных исследований сжимаемости элювиальных глинистых грунтов // Вопросы строительной механики. – Свердловск: УПИ, 1967. – С. 168 – 174.
- Бернацкий Л.Н. Прикладная геотехника. – М.: Трансжелдориздат, 1935. – 258 с.
- Алехин А.Н. Нелинейный анализ напряженно- деформированного состояния грунтовых массивов: Дисс…. канд. техн. наук/ Уральский политехнический институт. Свердловск, 1982. – 186 с.
- Алехин А.Н. Метод расчета осадок грунтовых оснований с использованием нелинейной модели // ″Реконструкция городов и геотехническое строительство″. – СПб., 2004. – № 8. – С. 156 – 161.
- Христофоров В.С., Задворнев Г.А. Напряженно-деформированное состояние грунта с нелинейными характеристиками при осесимметричной плоской деформации // Основания, фундаменты и механика грунтов. – 1978. - №6. – С. 19 – 21.
- Христофоров В.С., Задворнев Г.А. Определение прочностных и нелинейных деформационных характеристик несвязного грунта по результатам прессиометрических испытаний // Экспериментально-теоретические исследования процессов упругопластического деформирования оснований и фундаментов: Межвузовский сборник. – Новочеркасск: НПИ,1979. – С. 112 – 117.
- Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука,1979.– 285 с.
- Алехин А.Н., Соломин В.И. Решение прессиометрической задачи в нелинейной постановке // Основания и фундаменты в геологических условиях Урала: Межвузовский сборник научных трудов. – Пермь: ППИ, 1988. – С. 25 – 28.
- Hadamard J. Sur les problèmes aux dérivées partielles et leur signification physique. – 1902. – pp. 49–52.
- Alekhin A., Nikulin B. New developments in computer aided prediction of soil base settlements // Proceedings of the 4-th Intern. Conf. on Civil and Structural Engineering Computing. vol. 2. – London, Great Britain, 1989.. – pp. 249 – 254.
- Алехин А.Н. Определение параметров некоторых нелинейных моделей грунта по данным полевых испытаний // Инженерно-геологические проблемы урбанизированных территорий: материалы Международного симпозиума ″EngGeolCity-2001″. – Екатеринбург, Россия, 2001. – т. I. – С. 115 – 122.
- СП 50-101-2004. Проектирование и устройство оснований и фундаментов зданий и сооружений. – М.: Госстрой России, 2005. – 130 с.
- Малышев М.В. Прочность грунтов и устойчивость оснований сооружений. – М.: Стройиздат, 1994. – 227 с.
Записи на схожие темы

Превращаем отходы в чистоту: Революция в утилизации мусора
... и вывоз мусора, но и его дальнейшую переработку с целью сокращения ... контейнеры позволяет сократить расходы на его транспортировку и переработку, что особенно ... в поддержании чистоты, что доказывает его значимость для каждого жителя планеты.

Специалистам Россети-Урал представили современные решения по определению места повреждения ЛЭП
... практический семинар «Современные решения по определению и локализации мест повреждения в ... участникам семинара современное оборудование по определению и локализации мест повреждения в ...

ГК МК-Эталон провела проектно-экспертные работы по производственно-складскому комплексу по ул. Шефская в Екатеринбурге
... поработать со старыми знакомыми!:) В данном проекте нашей группой компаний проводились ... ! Надеемся на продолжение успешного сотрудничества! Параметры здания: Общая площадь здания - ...

Оборудование для мониторинга и диагностики ЛЭП презентовали экспертам Россетей
... спектра других задач, среди которых: определение повреждений на транзитных и отпаечных ... определять с точностью до ТП); определение сработавших линейных разрядников и ОПН ...

Нива лучший автомобиль в СССР
... одну из своих наиболее узнаваемых моделей - ВАЗ-2121, известную также ... в истории развития «Нивы» стали испытания и одобрение к производству е ... автомобилей. Важной вехой в истории модели стал 1995 год, когда ВАЗ ...

Бизнес на вендинговых аппаратах: стартап с потенциалом
... участия продавца, но и перспективная модель использования роботизированных механизмов в сфере ... аппарата во многом зависит от его расположения, подбор которого требует детального ... надёжных производителей и предпочесть модели с возможностью удалённого управления ...










Отправить комментарий